Алгоритм поиска пути. Игровой конструктор, часть 4

Один из важнейших кирпичиков любого игрового движка — модуль поиска путей. Он нужен в играх самых разнообразных жанров. В action pathfinding (именно этот устоявшийся термин используется в документации к разного рода движкам) поможет монстру максимально быстро найти героя или убежать от него, не запутавшись в четырех стенах. В стратегиях отряд лучников, которого неумолимая длань игрока послала на противоположный конец карты атаковать
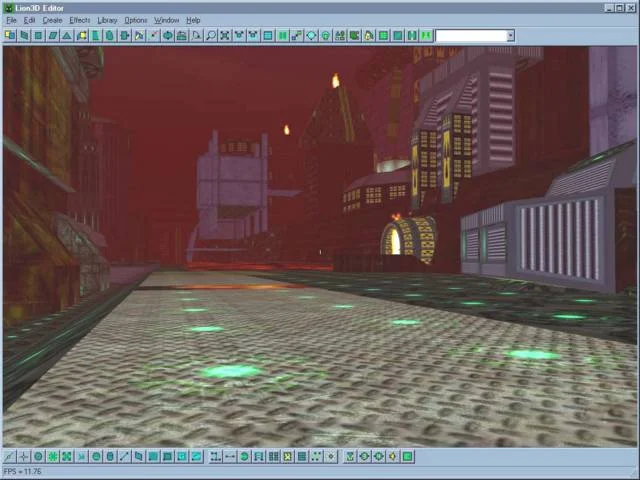
Система опорных точек в редакторе карт может быть такой. Опорные точки помечены зелеными кругами на земле.
вражескую крепость, в конце концов дойдет до нее, а не будет ходить по кругу у особо хитрого сочетания елочек и сосенок. В RPG партия приключенцев найдет священный Грааль, а не замрет у первой же стены. И даже в Lines храбрый шарик доберется до линии своих собратьев по цвету или же скажет, что это невозможно. Словом, модуль поиска путей нужен везде. А вот как его реализовать? Этим мы сейчас и займемся. Рождение матрицы Сначала слегка вас напугаю. Задачи, подобные этой, рассматриваются в дискретной математике и описываются теорией графов. Сама теория сопровождается водопадом заковыристых математических значков и такими страшными словосочетаниями, как “ отношение контрпозиции ”, “ эйлеров цикл ” и даже “ матрица весов ”. Но не придумали еще такой математической теории, которую нельзя было бы перевести на нормальный человеческий язык. Поэтому эта часть “Игрового конструктора” будет не сложнее остальных, а в чем-то даже и легче. Ведь мы, наконец, переходим к легко осязаемой практике. Прежде чем разбирать сами алгоритмы, сделаем важное замечание. Все алгоритмы поиска путей работают или с массивом, который отождествляет игровой мир, или со списком опорных точек — так называемых waypoints. Первый способ подходит для движков, у которых все объекты стоят строго в узлах воображаемой сетки и имеют одинаковые или кратные размеры. К ним относятся почти все тайтловые движки, движки разных классических игр и головоломок и даже движки стратегий с простой геометрией объектов. В них во всех карту игры можно представить в виде массива: Map:array[1…M,1…N] of integer; где MхN — размер карты в ячейках, а в каждой ячейке содержится цифра, соответствующая типу территории. Например: 1 — стена, пройти невозможно, 2 — ограда, пройти невозможно, но можно стрелять сквозь нее, 3 — забор, можно сломать и пройти, но на это затратится 5 элементарных единиц времени, 4 —

В изометрических движках список опорных точек может быть заменен на матрицу препятствий.
болото, можно пройти, но за 3 единицы времени на каждую клетку, 5 — ровная дорога, можно пройти за 1 единицу времени на каждую клетку, и так далее. Для стратегий с объектами сложной формы и всех нормальных экшенов карта представляется в виде совокупности waypoints. Каждую опорную точку можно представить в виде: PWaypoint=^TWaypoint; TWaypoint=record Position:TGLCoordinates; Connections:array of PWaypoint; Territory:integer; Radius:double; end; Первая строчка объявляет тип указателя на TWaypoint. В самой записи TWaypoint поле Position — координаты опорной точки, Connections — динамический массив с указателями на ближайшие опорные точки, в которые можно без препятствий дойти из этой точки, Territory — тип территории, на которой стоит опорная точка. Впрочем, этот параметр необязателен. Вы можете симулировать его, например, высотой того места, на котором стоит опорная точка. Последний необязательный параметр Radius показывает зону действия опорной точки, то есть на каком максимальном расстоянии может находиться юнит, чтобы считать себя стоящим на ней. Все опорные точки для одной карты лучше хранить в списке или динамическом массиве. Как создавать эти опорные точки — вопрос особый. Вы можете
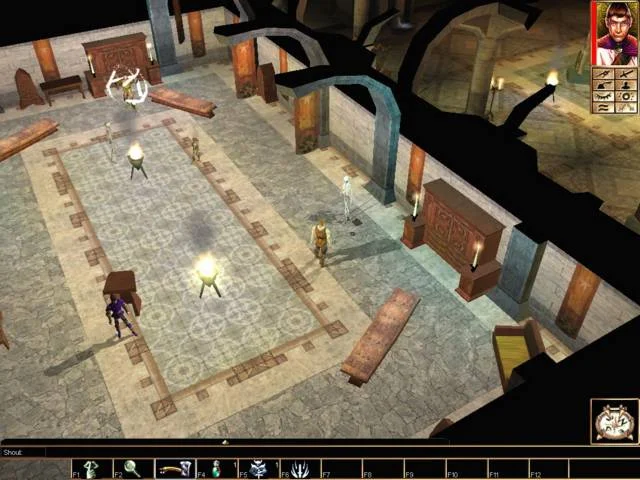
Хотя этот движок изометрический и спрайтовый, матрица препятствий тут бесполезна, потому что объекты имеют непостоянную форму.
предусмотреть для этого специальный инструмент в редакторе карт, чтобы дизайнеры уровней расставляли их вручную. Вы можете рассчитывать положение опорных точек автоматически при загрузке уровня, но дело это довольно сложное. Где ставить опорные точки — вопрос не менее интересный. У каждого из углов объекта, как внутренних так и внешних, чтобы юниты могли легко его огибать. В тупиках, узких проходах между объектами, в местах смены одного типа территории на другой — словом, везде, где нормальный человек сначала подумал бы, прежде чем идти дальше. Наконец, в центре больших открытых пространств, причем параметр Radius ставьте таким, чтобы он перекрывал большую часть этого пространства. В пределах этого круга юниты могут передвигаться свободно, по кратчайшей прямой, так как препятствий там нет. Теперь давайте перейдем к самим алгоритмам. На гребне волны… Один из самых простых для понимания алгоритмов поиска путей и вместе с тем довольно эффективный — волновой поиск. Он идеально подходит для небольших карт, которые можно представить в виде двумерного массива ячеек. Для начала вам нужно завести еще один двумерный массив целых чисел такого же размера, как и основной массив карты. Алгоритм работает следующим образом. Находим точку А, из которой начинается поиск, и в этом месте в
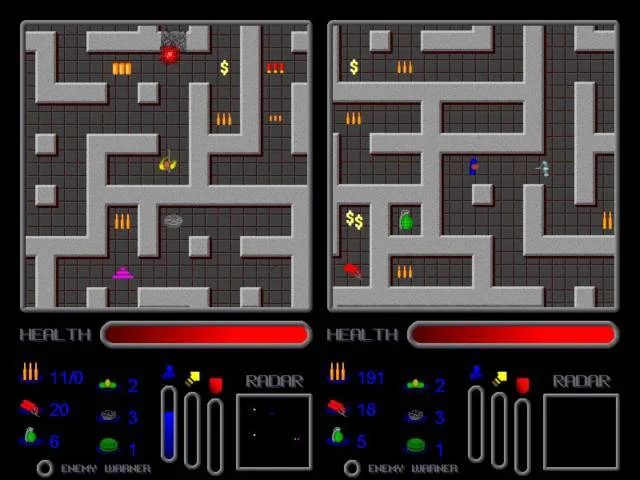
В играх-головоломках и аркадах чуть сложнее «Диггера» прекрасно работает волновой алгоритм поиска.
вспомогательном массиве ставим 0. Во всех свободных ячейках, которые прилегают к ячейке с нулем, пишем 1. Во всех свободных от цифр и препятствий ячейках, которые прилегают к ячейкам с 1, пишем 2. Повторяем этот процесс для всех остальных ячеек, пока не дойдем до ячейки B, путь до которой нам требовалось найти. Если вы визуализируете этот процесс в динамике, то увидите, что от точки A разбегается волна из цифр. Отсюда и название алгоритма. Как только наша цифровая волна захлестнет точку B, строим от нее путь до точки A по правилу: следующая точка пути должна лежать в ячейке с меньшим, чем в текущей ячейке числом. Алгоритм неплохо справляется с разного рода тупиками и всегда найдет путь из A в B, если он вообще существует. Другое дело, что этот путь редко будет кратчайшим из возможных. К сожалению, волновой поиск нельзя использовать на больших картах (с десятком тысяч и более клеток), так как он работает очень медленно. Поиск в глубину Предыдущий алгоритм иногда называют поиском в ширину , потому что он уровень за уровнем просматривает ближайшие клетки. Поиск в глубину выбирает какое-то одно направление и просматривает его вглубь на заданное число клеток, переходит к следующему направлению и так далее, пока не найдет конечную точку. Представленная ниже рекурсивная функция находит не все возможные пути. Чтобы найти кратчайший путь, надо вызвать эту функцию для каждой из клеток, прилегающих к начальной клетке. Во вспомогательном булевом массиве Mark такого же размера, как и остальная карта, хранится 1, если текущая клетка уже пройдена алгоритмом, и 0 — в противном случае. В переменных Destination_x и Destination_y должны храниться координаты точки, куда в итоге надо попасть. В глобальной перемененной Length будет храниться длина текущего пути, чтобы мы не залетели вглубь матрицы дальше, чем MAX_LENGTH.Procedure DepthSearch(x,y:integer); Var i : integer;
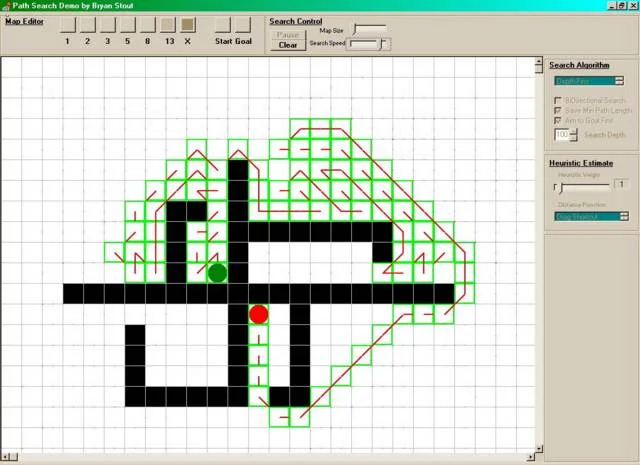
Визуализация алгоритма поиска в глубину с максимальной длиной пути — 100 клеток. Алгоритм нашел короткий, но далеко не самый кратчайший путь.
Begin If Length >MAX_LENGTH then exit; Mark[x,y] := True; If (x=Destination_x) and (y=Destination_y) then Begin { Мы нашли эту точку! Искомый путь представлен значениями True в массиве Mark. Здесь вы можете запомнить построенный путь и очистить Mark[x,y], чтобы продолжить поиск, или же остановиться, если задачей было найти хотя бы один путь.} End; Length:=Length+1; If Mark[x+1,y]=false then DepthSearch(x+1,y); If Mark[x,y+1]=false then DepthSearch(x,y+1); I f Mark[x+1,y+1]=false then DepthSearch(x+1,y+1); If Mark[x-1,y-1]=false then DepthSearch(x-1,y-1); If Mark[x-1,y]=false then DepthSearch(x-1,y); If Mark[x,y-1]=false then DepthSearch(x,y-1); Length:=Length-1; End; В некоторых случаях этот алгоритм работает быстрее, чем волновой, но у него есть свой недостаток: если точка, путь до которой надо найти, находится дальше, чем MAX_LENGTH, алгоритм ее не найдет. Можно снять это ограничение, но тогда появится опасность зацикливания. Поиск в глубину хорошо работает в случае больших лабиринтов с узкими проходами. На широких открытых пространствах лучше использовать поиск в ширину. Алгоритм Дейкстры Алгоритм Дейкстры выигрывает у всех предыдущих алгоритмов как по скорости, так и по качеству поиска. Его легко адаптировать как для клетчатых полей, так и для списков опорных точек. Он берет в расчет весовые коэффициенты связей между точками. То есть с его помощью можно рассчитывать пути на картах с разными типами местности и с учетом расстояния между опорными точками. Минус у него только один: относительная сложность реализации, хотя по принципу действия он очень похож на поиск в ширину. Из-за того, что в нем используется приоритетная очередь , его реализация для разных задач будет разной. Поэтому я приведу только псевдокод, а в конце дам советы, как этот псевдокод превратить в код реальный, исходя из того, что вам нужно.Приоритетная очередь Open

В спортивных симуляторах используются одни из самых сложных алгоритмов поиска путей — интегрированные с AI.
DijkstraSearch Опорные точки n, n’, s s.cost = 0 s.parent = null // s — точка начала поиска Занести s в Open Пока Open не пуст Извлечь точку n из Open Если n — цель поиска, построить путь и выйти из алгоритма Для каждой точки n’ смежной с n newcost = n.cost + cost(n,n’) Если n’ находится в Open и n’.cost <= newcost прервать текущую итерацию и перейти к следующей n’.parent = n n’.cost = newcost Если n’ не содержится в Open занести n’ в Open Путь не найден Open — это приоритетная очередь, то есть список вершин, который остается отсортированным по расстоянию вершин от начальной точки после любой операции. Его можно реализовать списком TList и тогда несложно воспользоваться его свойством Sorted. Однако для некоторых задач удобнее представить приоритетную очередь в виде динамического массива опорных точек и при добавлении нового элемента следить за тем, чтобы порядок сортировки не нарушался. В некоторых средах и языках программирования есть отдельные классы, которые реализуют приоритетную очередь. Тогда вы можете воспользоваться ими. Функция Сost рассчитывает весовой коэффициент между точками n и n’. В простейшем случае это будет расстояние между двумя точками, ну а в сложном можно учитывать такие вещи, как тип местности, время разворота юнита в нужном направлении, затраты энергии и много чего еще.
*** * *** Мы рассмотрели базовые алгоритмы поиска пути. За бортом остались такие интересные вещи, как “звездный” алгоритм A*, потенциальные поля, трассировка пути и, конечно же, тонкости реализации всех этих алгоритмов в GLScene. Все эти вопросы мы обязательно затронем в одной из статей цикла.