Партия Сусанина. Игровой конструктор, часть 5

В прошлый раз мы рассмотрели базовые алгоритмы поиска пути. Теперь конница не петляет между деревьями в лесу, а мчится во весь опор через чистое

Поисковые алгоритмы можно применять не только для поиска путей между реальными препятствиями, но и между виртуальными ограничителями, например между возможными зонами падения и перехвата мяча.
поле наперерез условному противнику. А полякам больше не требуется помощь Ивана Сусанина, они и сами дорогу знают. И все бы ничего, да вот процессор разрывается между десятками задач. Ему и спецэффекты модные рассчитать надо (не все же видеокарте трудиться), и уровень динамически обновить, и каждому юниту на поле брани искусственный затылок почесать, соображалку завести. А тут еще пути рассчитывать приходится… Вот и дымится процессор от такого непосильного бремени. А то еще маркетологи наседают, заявляют, иноверцы, что если на экране одновременно меньше ста тысяч юнитов — им стыдно начальству в глаза смотреть. Вот и приходится программистам измышлять другие способы для поиска путей. А вот какие — это мы сейчас и узнаем. **Гори-гори, моя звезда…*Звездой поисковых алгоритмов программисты между собой называют алгоритм со странным названием A. На первый взгляд он очень похож на алгоритм Дейкстры , который мы рассмотрели в прошлый раз. А работает во много раз быстрее и эффективнее. Секрет — в особой эвристике определения качества найденного пути. Каждой точке пути алгоритм присваивает весовой коэффициент f(n) , который можно определить так:

В качестве препятствия на пути игрока может быть не только стена или овраг, но и монстр.
f(n) = g(n) + Н(n) Здесь g(n) — это цена пути из начальной точки поиска в текущую. Цена пути определяется точно так же, как и в алгоритме Дейкстры. В простейшем случае это сумма евклидовых расстояний между всеми точками пути. Вы можете взять в расчет местность, по которой пролегает путь, расстояние до объектов, которых надо опасаться (врагов). Вторая часть суммы — Н(n) — это примерная (эвристическая) цена пути из текущей точки в конечную. Как же определить эту цену, если и самого пути-то еще нет? В этом и заключается основная хитрость. Представьте себе, что в дальнейшем путь будет обладать такими же характеристиками, как и раньше. Например, вы все время шли по гористой местности и приходилось один раз обходить лагерь врагов. Значит, вполне возможно, что и
Одно из преимуществ алгоритма A* — вы можете задать не одну, а сразу несколько целей для поиска.
оставшаяся часть пути будет не менее гористой, да и еще один лагерь попадется. Это предположение может быть неверным — например, сразу после текущей точки начнется ровное поле. Но представьте, что наше предположение верно. Статистика — замечательная штука. Из этого самого предположения рассчитайте кратчайший путь до конечной точки. Если карта игры у вас двумерная, достаточно определить длину прямой, соединяющей текущую и конечную точки. Умножьте эту длину на среднюю “тяжесть” пути, и, вуаля, готова эвристическая цена оставшегося пути. Алгоритм A* дает потрясающие результаты за относительно небольшое время, но… только если вы правильно подобрали функцию эвристической оценки. Чем лучше эта функция, тем точнее и быстрее найдется нужный путь. Более того, если для выбранной системы координат и представления игрового пространства вы используете оптимальную эвристическую функцию, найденный путь будет гарантированно кратчайшим из всех возможных. Управляя весовыми коэффициентами каждой конкретной точки карты, вы можете легко добавлять критерии поиска. Например, вы захотели поощрять искусственный интеллект исследовать еще некоторые территории. Просто добавьте к весовым коэффициентам неоткрытых точек определенный бонус, и тогда управляемый ИИ исследователь из всех кратчайших путей к нужной точке будет отдавать предпочтение тем, которые приводят к открытию новых земель. Точно так же вы можете дать задание шпиону уклоняться от вражеских патрулей или утлому суденышку опасаться быстрого течения на стержне реки. Совсем необязательно давать A* задание искать путь только в какую-то одну определенную точку. Вы можете задать целый набор точек. Тогда Н(n) в каждой точке будет определяться как минимальная цена пути среди путей ко всем точкам назначения. Давайте взглянем на детализованный алгоритм A* : _

_
Зелено-черный градиент — это потенциальное поле. Точки старта и финиша в левом верхнем и правом нижнем углах соответственно.
//s — точка, из которой начинаем поиск s.g = 0 //Вычисляем эвристическое расстояние до конечной точки s.Н = GoalDistЕstimatе( s ) s.f = s.g + s.Н s.рarеnt = null Поместить s в очередь Oреn Пока список Oреn не пуст Извлечь точку n из Oреn Если n -финальная точка Построить путь //Алгоритм успешно отработал Выход Для каждого наследника n’ от n nеwg = n.g + cost(n,n’) Если (n’ находится в Oреn или Closеd) _и (n’.g <= nеwg) _ Пропустить n’.рarеnt = n n’.g = nеwg n’.Н = GoalDistЕstimatе( n’ ) n’.f = n’.g + n’.Н Если n’ находится в _ Closеd _ Удалить n’ из Closеd Если n’ еще не находится в Oреn Поместить n’ в Oреn Поместить n в Closеd Выход // Путь не найден Oреn — это все та же приоритетная очередь, хорошо знакомая вам по алгоритму Дейкстры. Здесь появился новый список — Closеd. Он не обременен

Одно из преимуществ потенциального поля: вместо того чтобы обойти препятствие по его границе, алгоритм предпочел держаться от него подальше (синяя линия).
никакими дополнительными условиями — это просто список без всяких приоритетов. Поэтому вы можете реализовать его как с помощью TList , так и с помощью динамических массивов. Он предназначен для того, чтобы исключить повторную обработку точек, которые уже включались в путь на данном этапе поиска. Потенциальные поляУ каждого из алгоритмов поиска путей, которые мы рассматривали, есть свои достоинства и два общих недостатка. В случае, если игровое поле представляет собой не лабиринт, а множество разрозненных препятствий, пусть и размещенных сколь угодно затейливо, алгоритмы будут работать неоправданно долго. Еще одна проблема: рассчитанные пути очень часто пролегают слишком близко к краям препятствий. Путь юнита по такому маршруту будет выглядеть неестественно. А иногда такое поведение противоречит логике игры. Например, вражеский юнит обходит свое минное поле по периметру. Вы об этом минном поле, естественно, не знаете. Представьте картину: вражеский юнит бежит в атаку на ваше воинство, вдруг резко меняет направление, оббегает какой-то призрачный прямоугольник и бежит дальше. Есть повод задуматься! И самое главное — без дополнительных изменений алгоритмов путь придется рассчитывать после каждого хода, если ситуация на игровом поле постоянно меняется. А такое происходит сплошь и рядом.
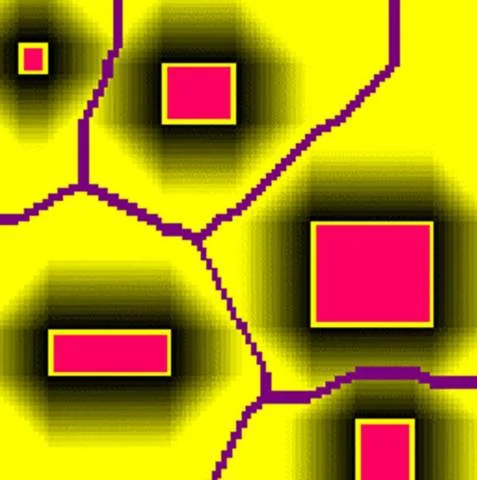
Каждое препятствие создает вокруг себя свое потенциальное поле. Фиолетовые участки — локальные минимумы, по которым с наибольшей вероятностью пойдет юнит.
В таких ситуациях хорошо себя зарекомендовали так называемые потенциальные поля. Каждой точке на карте присваивается свой весовой коэффициент — потенциал согласно какому-то условию. Пусть, например, чем ближе точка к цели поиска, тем выше у нее потенциал. Тогда у точки, из которой начинается поиск, потенциал будет самым низким. Запрограммируйте юнита все время двигаться из точек с меньшим потенциалом к точкам с большим — и вы увидите интересную картину. Точка старта будет как бы отталкивать юнит, а точка назначения, наоборот, притягивать. Мысленно поместите в точку старта мощный магнит северным концом, в точку назначения — еще более мощный магнит южным, а юнит представьте маленьким магнитиком, который отталкивается от первого магнита и притягивается ко второму. Но на игровом поле пока нет никаких препятствий. Если мы поместим прямоугольное препятствие на пути юнита, он, повинуясь закону о разности потенциалов, проскользит вдоль одного из его краев и пойдет себе дальше. А если препятствие сделать в форме угла? Юнит в нем просто застрянет. Вот мы и подошли к самой интересной особенности потенциальных полей! Каждое препятствие — это тоже магнит, который отталкивает от себя юнит! Причем чем больше и опаснее препятствие, тем сильнее отталкивающая сила. Теперь юнит от точки старта до точки назначения будет двигаться как будто по фарватеру, между всеми возможными препятствиями и опасностями. С точки зрения игрока, путь, который выберет юнит, будет самым естественным. А ведь реализм — одна из главнейших характеристик любой игры. Алгоритм потенциальных полей очень похож на волновой алгоритм, который мы рассмотрели в прошлый раз. Вот только волны выпускаются не только из начальной точки, но и из всех препятствий. Реализовать этот алгоритм так же просто. Однако в целях оптимизации разделите все потенциальное поле карты на две части. Первая часть — поле, которое создают точки старта и назначения, ну а вторая — объединение всех полей препятствий. Дело в том, что при каждом новом поиске пути начальные и конечные точки меняются, а значит, меняются и их потенциальные поля. Ну а поля препятствий все время остаются неизменными. Перед каждым новым поиском просто сложите две этих части, и получите готовую потенциальную карту пути, по которому должен пойти юнит. Алгоритм потенциальных полей находит не всегда самый кратчайший путь, но уж точно самый красивый и естественный.

Программирование для начинающих __ Этой статьей мы заканчиваем цикл статей по движку GL-Scene. Данные материалы изначально были ориентированы на продвинутых игростроевцев, уже знакомых с азами Delphi. В одном из ближайших номеров (возможно, уже в следующем) стартует новый цикл по программированию игр и программ, но ориентированный на начинающих игроделов. Каждая статья будет представлять собой детальное руководство по созданию какой-то одной утилиты или игры. Даже если до этого вы ни разу не сталкивались с программированием, вы без труда сможете разобраться, что к чему.
*** * ***Мы рассмотрели самые популярные, самые передовые алгоритмы поиска путей. Конечно, разработчики редко используют их “в чистом виде”, а добавляют свои авторские корректировки согласно цели. Теперь, зная принципы действия этих алгоритмов, вы сами без труда приспособите их для игры любого жанра.